I. Testaufbau

Eine Kontingenztabelle wird erstellt. Dabei werden die in der spezifischen Bank beobachteten Ausfälle (B) mit den aus dem Vergleichspool erwarteten Ausfällen (E) verglichen. E pro Ratingklasse berechnet sich wie folgt: \[E = \frac{\text{Anzahl Ausfälle in Vergleichspool}}{\text{Anzahl Schuldner in Vergleichspool}}\cdot \text{Anzahl Schuldner in spezifischer Bank}.\] Die Kontingenztabelle hat dann folgendes Aussehen:

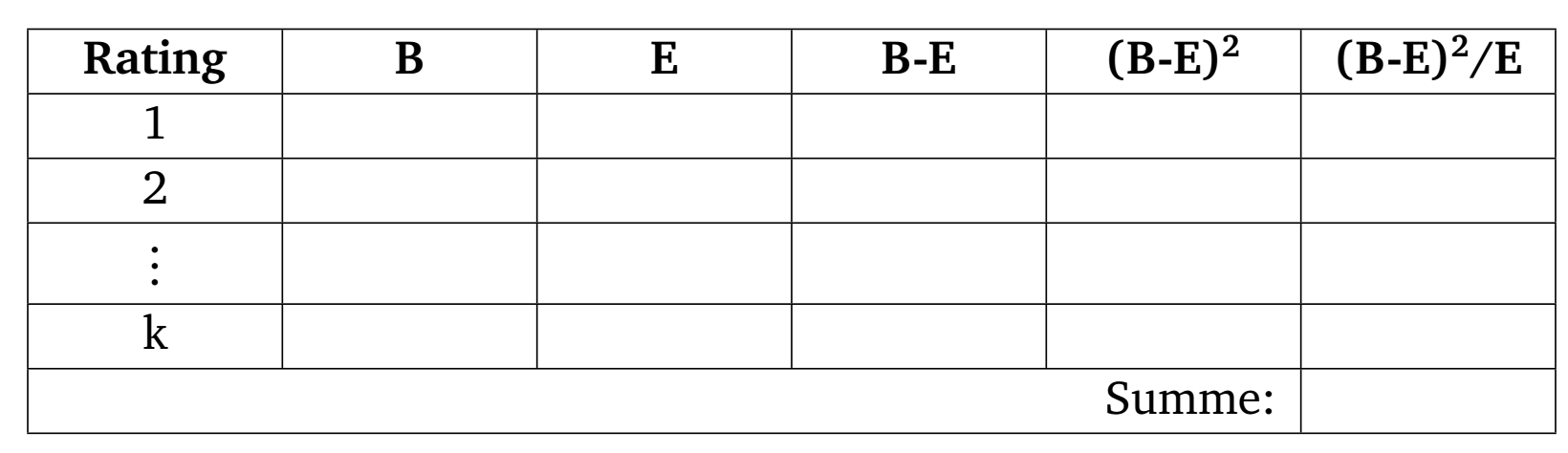
Die Summe \(\sum_{i=1}^k (B_i-E_i)^2/E_i\) über alle relevanten Ratingklassen ist die Teststatistik. Sind im Vergleichspool für eine Ratingklasse keine Ausfälle aufgetreten, wird diese Klasse mit der nächsten Ratingklasse zusammengefasst. Ratingklassen, für die es in der spezifischen Bank keine Schuldner gibt, werden ausgelassen. Die verbleibenden bzw. zusammengefassten Ratingklassen definieren die \(k\) Zeilen der Kontingenztabelle.

II. Hypothesen

Folgende Hypothesen werden getestet:

Nullhypothese (\(H_0\)): Es gibt keinen Unterschied in der Verteilung der Ausfälle zwischen der spezifischen Bank und dem Gesamtpool – die Ausfallmuster der spezifischen Bank sind repräsentativ für den Gesamtpool.

Alternative Hypothese (\(H_a\)): Es gibt einen signifikanten Unterschied in der Verteilung der Ausfälle zwischen der spezifischen Bank und dem Gesamtpool – die Ausfallmuster der spezifischen Bank sind nicht repräsentativ.

III. Durchführung des Tests

Mit der Teststatistik aus der Kontingenztabelle wird der Chi-Quadrat-Test durchgeführt, um zu überprüfen, ob die Unterschiede in den beobachteten Häufigkeiten der Ausfälle zwischen der spezifischen Bank und dem Gesamtpool größer sind, als man zufällig erwarten würde. Hierzu wird die Teststatistik \(\tilde{T}=\sum_{i=1}^k (B_i-E_i)^2/E_i\) als \(\chi^2\)-verteilte Zufallsgröße mit \(k-1\) Freiheitsgraden betrachtet und der P-Wert über die entsprechende kumulierte Verteilungsfunktion berechnet (P-Wert =\(1-\chi_{k-1}^2(X\leq\tilde{T})\)).

IV. Interpretation

Ein signifikantes Testergebnis (typischerweise ein \(P\)-Wert kleiner als 0,05) würde darauf hinweisen, dass die Verteilung der Ausfälle in der spezifischen Bank signifikant vom Gesamtpool abweicht.

V. Anmerkungen

Datenentfernung: Wenn die Daten der spezifischen Bank bereits im Gesamtpool enthalten sind und einen signifikanten Anteil des Pools ausmachen, könnte dies die Ergebnisse verzerren. Eine Entfernung der Daten der spezifischen Bank aus dem Gesamtpool vor dem Vergleich könnte notwendig sein, um eine unabhängige Bewertung zu gewährleisten.

Datengröße und -verteilung: Die Zuverlässigkeit des Chi-Quadrat-Tests kann durch die Größe der Stichproben und die Verteilung der Daten beeinflusst werden. Insbesondere sollten die erwarteten Häufigkeiten in den Zellen der Kontingenztafel nicht zu klein sein.

Anforderungen an die Stichprobe: Idealerweise sollten die Stichproben als Ganzes nicht zu klein und die der Nullhypothese entsprechenden erwarteten Häufigkeiten \(E\) nicht unter 1 liegen (\(E > 1\)). Sind sie kleiner, so werden sie durch Zusammenlegen von benachbarten Klassen auf das geforderte Niveau erhöht. Dies ist aber nur dann nötig, wenn die Anzahl der Klassen klein ist. Für den Fall \(k \approx 9\) und einem nicht zu kleinen Stichprobenumfang \(n \approx 40\) dürfen die Erwartungshäufigkeiten in vereinzelten Klassen unter 1 absinken (vgl. (Sachs 2004), [43], vorletzter Absatz, p. 422).

systematische Fehler: Die Vorzeichen der Differenzen \(B - E\) sind zu beachten. Idealerweise sollten \(+\) und \(-\) sich miteinander abwechseln und keine systematischen Zyklen zeigen (vgl. (Sachs 2004), [43], letzter Absatz, p. 422).

IV. Beispiel

Ausgangspunkt ist folgende Datenlage:

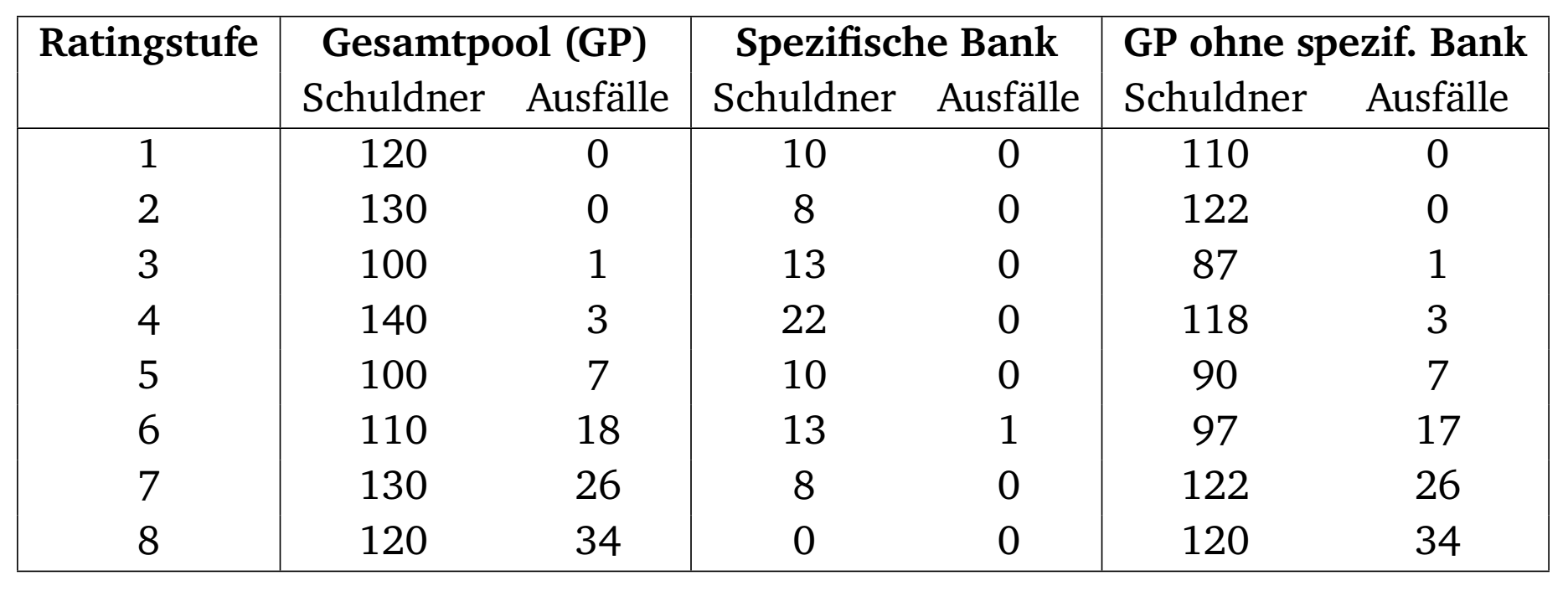
Als Vergleichspool wird der Gesamtpool ohne die spezifischen Bankdaten verwendet. Nachdem in den ersten beiden Ratingklassen keine Ausfälle im Vergleichpool auftraten, werden die ersten 3 Klassen zusammengefasst. Die spezifische Bank hat keine Schuldner in Ratingklasse 8. Diese wird daher nicht betrachtet. Die Kontingenztabelle hat damit folgende Form:

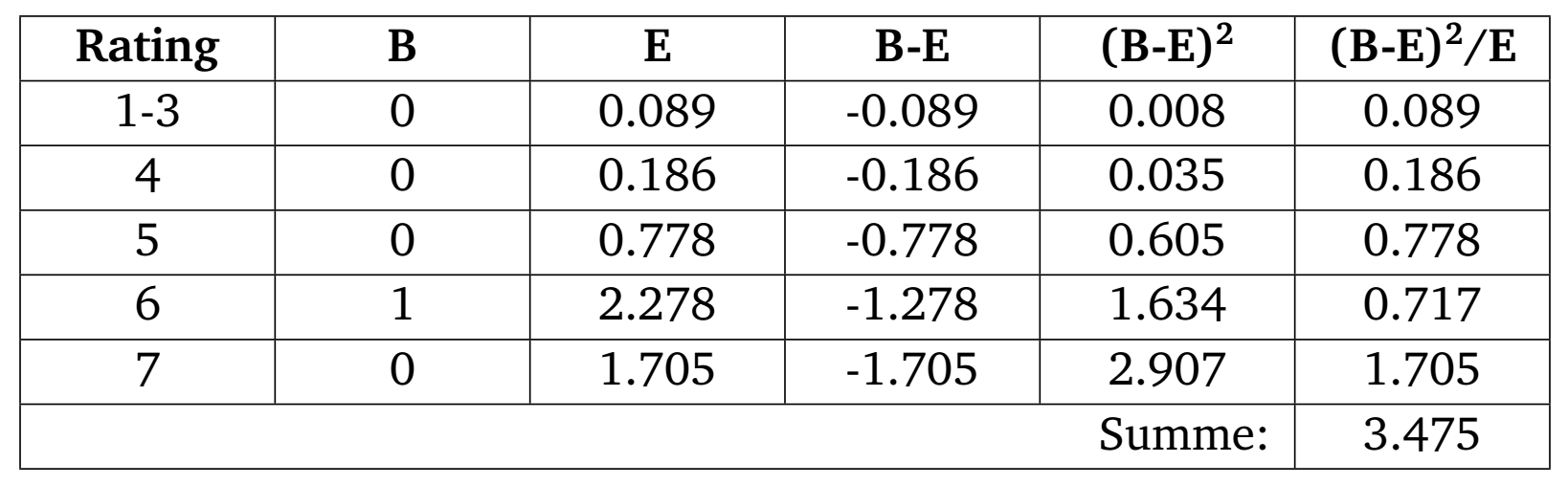
Dabei wird beispielsweise E für die Ratingklasse 5 folgendermaßen berechnet: \[\begin{aligned} E & = \frac{\text{Anzahl Ausfälle in Vergleichspool}}{\text{Anzahl Schuldner in Vergleichspool}}\cdot \text{Anzahl Schuldner in spezifischer Bank}\\ & = \frac{7}{90}\cdot 10\\ & = 0.778 \end{aligned}\] Die Tabelle hat 5 Zeilen. Daher wird die Teststatistik \(3.475\) mit der \(\chi^2\)-Verteilung mit 4 Freiheitsgraden verglichen. Es ist \[\text{P-Wert} =1-\chi_{4}^2(X\leq 3.475) = 0.482.\] Der P-Wert liegt über einem vorgegebenen \(\alpha=0.05\). Die Aussage \(H_a\), dass es einen signifikanten Unterschied in der Verteilung der Ausfälle zwischen der spezifischen Bank und dem Gesamtpool gibt, kann somit nicht empirisch bestätigt werden, d.h. sie ist statistisch nicht signifikant. Die Nullhypothese wird daher nicht abgelehnt.

Die Vorzeichen von \(B-E\) sind alle negativ (vgl. Anmerkungen 2, letzter Absatz). Der Test schließt zwar, dass die Nullhypothese nicht widerlegt werden kann, allerdings liegt die Vermutung nahe, dass die spezifische Bank tendenziell ein leicht besseres Portfolio als der Vergleichspool aufweist.

Literatur

Sachs, Lothar. 2004. Angewandte Statistik, 11nd Ed. Berlin: Springer.