Im klassischen Binomialtest werden Ausfälle innerhalb einer
Ratingklasse als unabhängig voneinander betrachtet. Für die \(N\) Schuldner innerhalb einer Ratingklasse
handelt es sich damit um \(N\)
unabhängige Bernoulli-Experimente \(X_i\) mit \(P(X_i=1)=\text{PD}\) und \(P(X_i=0)=1-\text{PD}\) für alle \(i=1, \dots, N\). Die Anzahl der Ausfälle
aus diesen \(N\) Bernoulli-Experimente
ist Binomialverteilt, d.h. ist \[
X = X_1 + \dots + X_N\] die Zufallsgröße für die Anzahl der
Ausfälle in der zu validierenden Ratingklasse, so gilt für den \(P\)-Wert: \[\text{P-Wert} = P(X \geq D) = \sum_{i=D}^{N}
\binom{N}{i} \text{PD}^i (1-\text{PD})^{N-i}.\] Dabei ist \(D\) die Anzahl der beobachteten
Ausfälle.
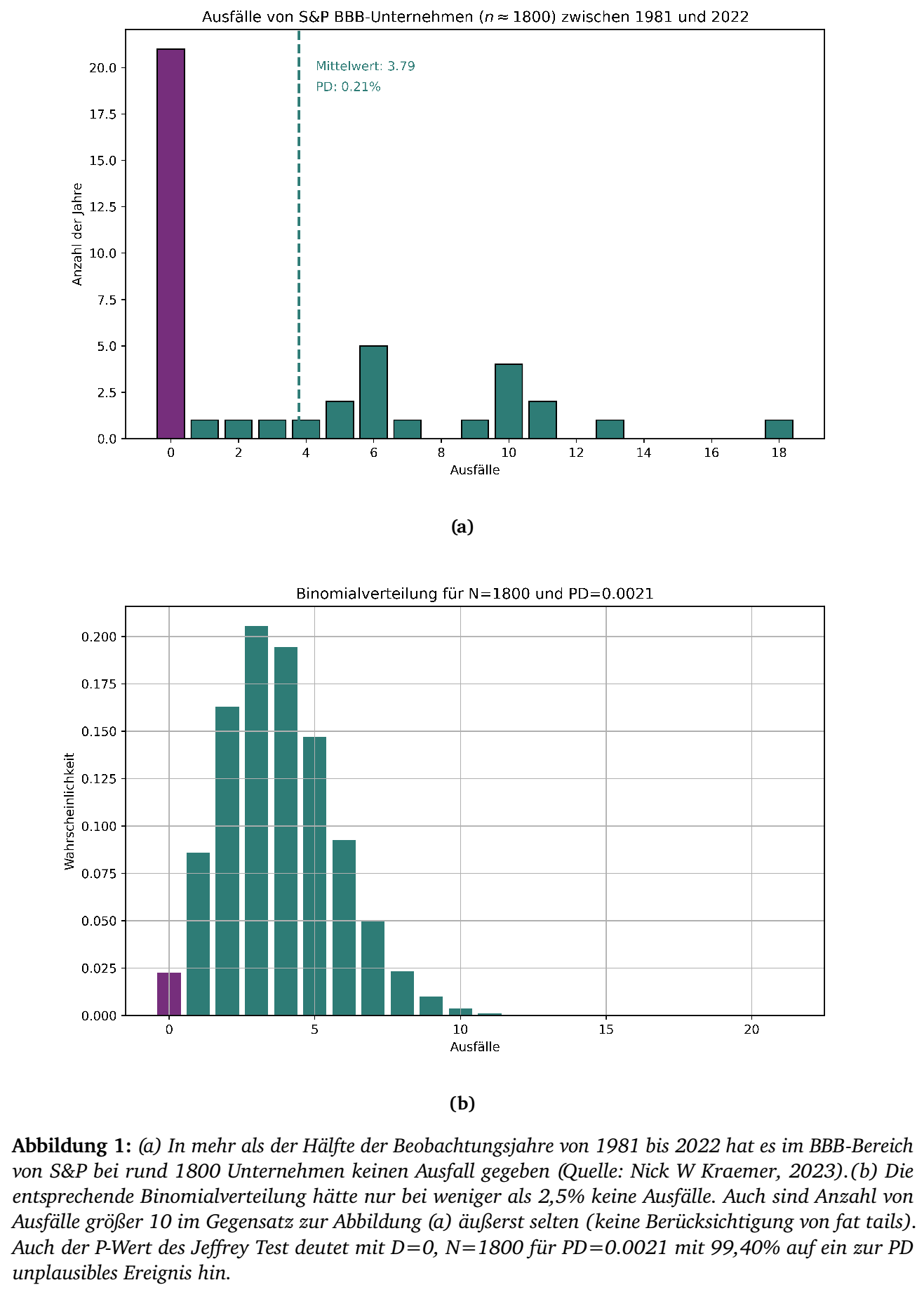
Die Unabhängigkeit der Ausfälle ist keine plausible Annahme und
verfälscht das tatsächliche Bild für die Wahrscheinlichkeit, dass selbst
in einer "’schlechten"’ Ratingklasse keine Ausfälle auftreten. So zeigt
die Auswertung der BBB-Schuldner von S&P, dass kein Ausfall eher die
Regel als die Ausnahme ist (vgl. Abbildung 1).
Beta-Binomialverteilung
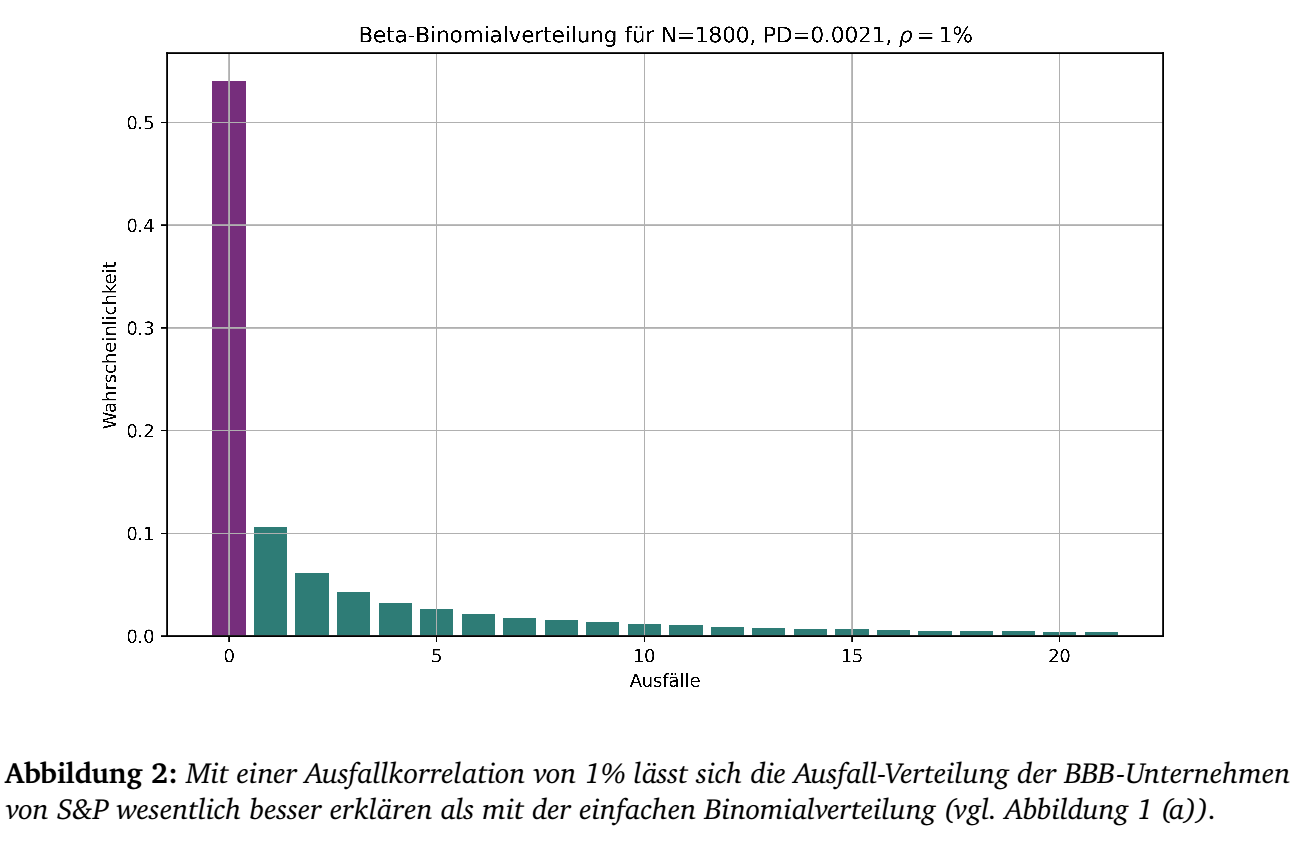
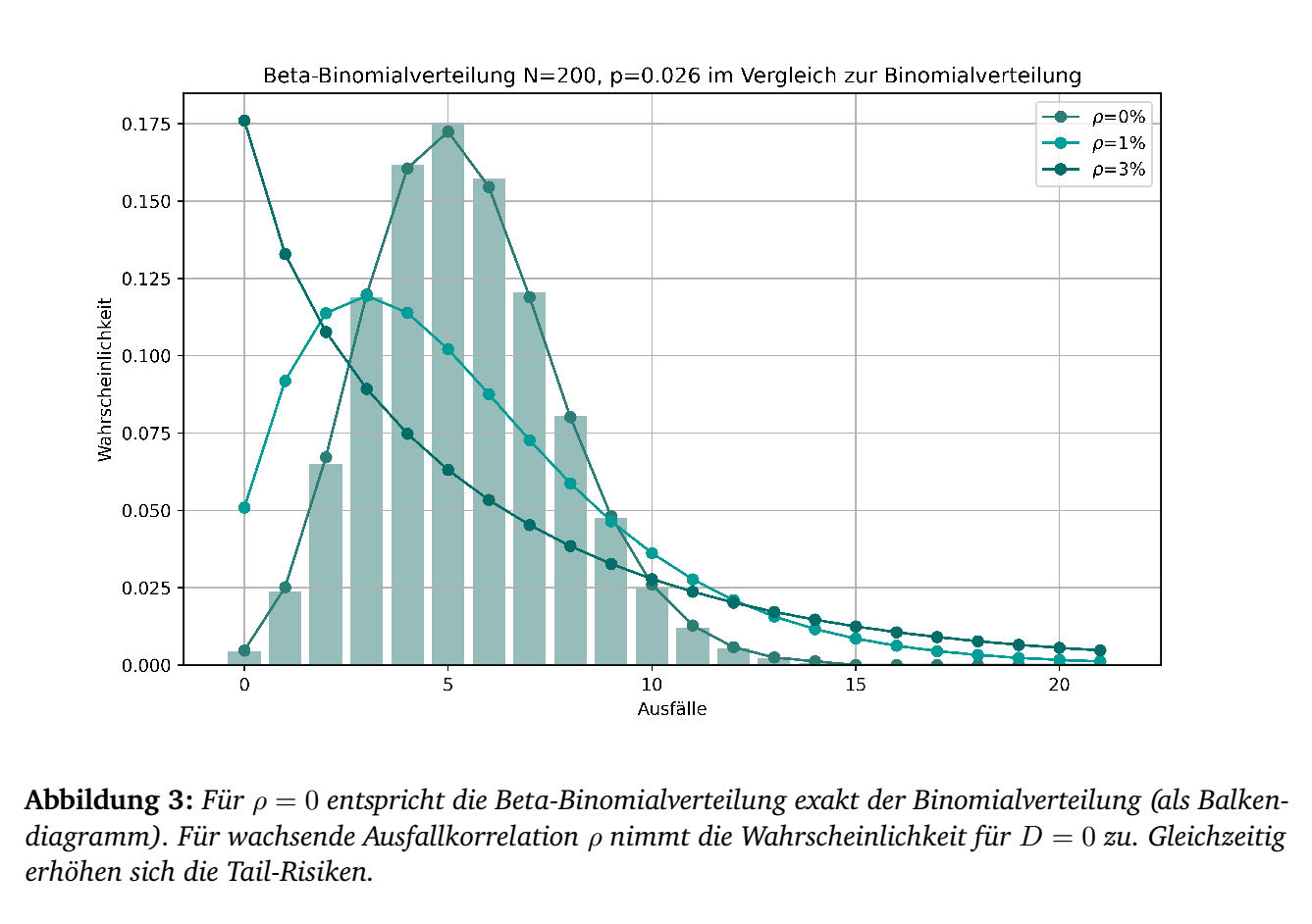
Die Beta-Binomialverteilung ist - wie der Name andeutet - eine
Kombination aus der Beta-Verteilung und der Binomialverteilung. Es
verallgemeinert die Binomial-Verteilung indem es Variationen in der
Ausfallwahrscheinlichkeit zulässt. Die Wahrscheinlichkeit für das
Auftreten von \(k\) Ausfällen ist mit
der Beta-Binomialverteilung \[P(X=k) =
\binom{N}{k} \frac{B(\alpha+k, \beta + N -
k)}{B(\alpha,\beta)}.\] Dabei ist \(B(\alpha, \beta)\) die Beta-Funktion.
\(X\) kann analog zur klassichen Binomialverteilung
auch als die Summe von \(N\)
Bernoulli-Experimente \[X = X_1 + \dots
X_N\] mit einheitlicher Ausfallwahrscheinlichkeit \(\frac{\alpha}{\alpha+\beta}\) aufgefasst
werden. Allerdings gibt es nun (vgl. (Leonhard Held 2020), p. 141-142) eine
Korrelation zwischen den einzelnen Bernoulli-Variablen in Höhe von \[\rho(X_i,X_j) =
\frac{1}{\alpha+\beta+1}.\] Um die Beta-Binomialverteilung
sinnvoll nutzen zu können, müssen \(\alpha\) und \(\beta\) so kalibriert werden, dass sowohl
die PD der entsprechenden Rating-Klasse als auch eine gegebene
Ausfallkorrelation \(\rho\) innerhalb
der Ratingklasse übereinstimmt. Dazu wählt man (vgl. (Moraux 2010), p. 68, (3))
\[\alpha=\text{PD} \cdot
\frac{1-\rho}{\rho}\] und \[\beta=(1-\text{PD}) \cdot
\frac{1-\rho}{\rho}.\] Damit ist der Erwartungswert der
Beta-Binomialverteilung \[E[X] = N \cdot
\frac{\alpha}{\alpha+\beta} = N \cdot \text{PD}\] und die
Korrelation \[\rho(X_i,X_j) = \frac{1}{\alpha+\beta+1} =
\rho.\]
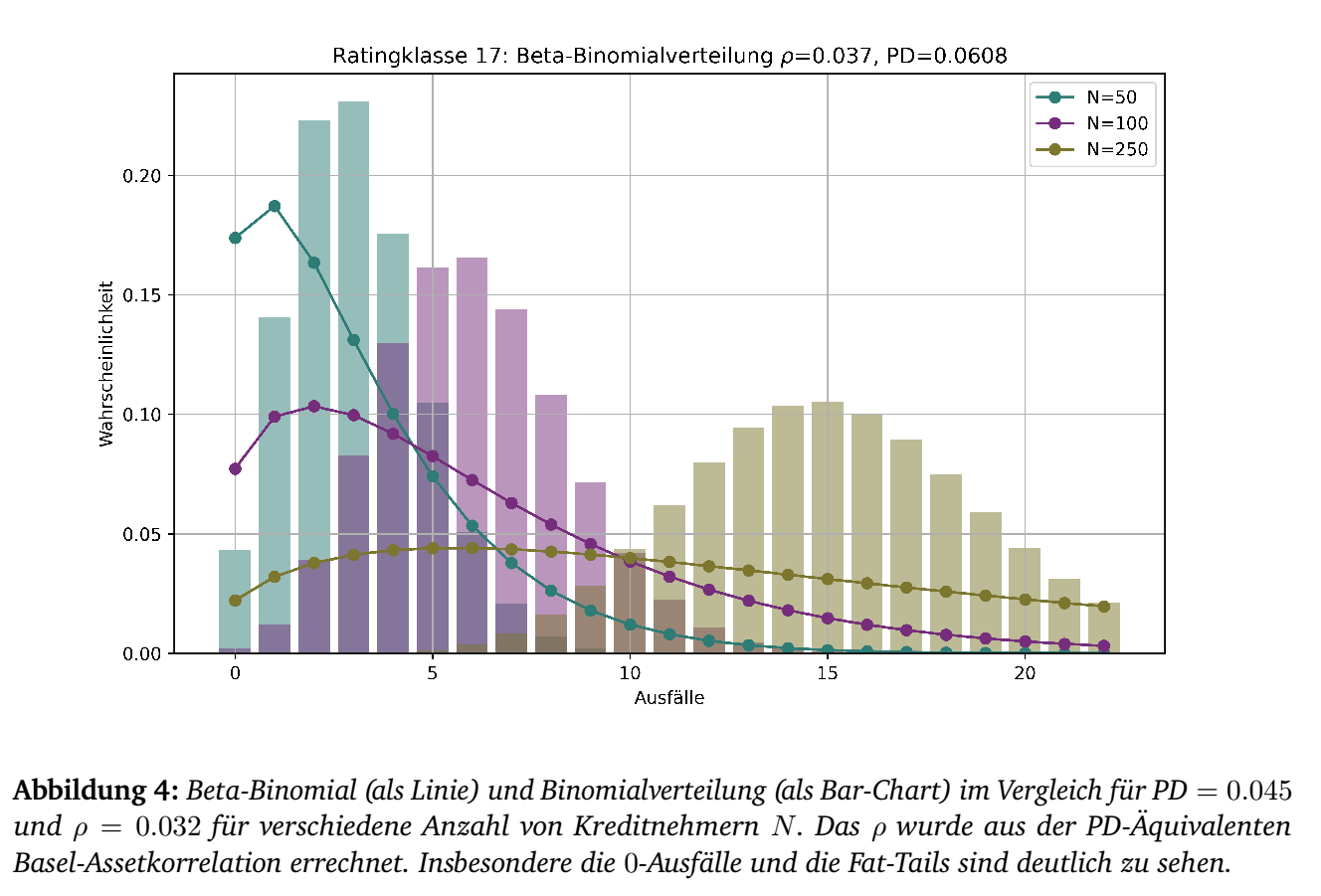
Korrelationen aus Basel III
Die in Basel III beschriebenen Korrelationen (vgl. (BIS CRE 2023)) sind Assetkorrelaionen. Das für Basel verwendete 1-Faktormodell ist ein Firmenwertmodell, das als Faktor die Abhängigkeit zum systematischen Markt benutzt. Um diese für das Beta-Binomialmodel zu nutzen, müssen diese in Default-Korrelationen umgewandelt werden. In (Andreas Henking 2006), 6.1.3, pp. 166-167 wird hierzu eine Formel angegeben. Diese ermöglicht es, das Beta-Binomialmodell konsistent zur vorgegebenen Eigenmittelunterlegung zu verwenden.
Umsetzung in Excel
Die Umsetzung der Beta-Binomialvetrteilung in Excel hängt im Wesentlichen von der Beta-Funktion \(B(\alpha,\beta)\) ab. Diese ist in Excel nicht verfügbar, kann aber über einen Umweg über die Betaverteilung berechnet werden. Als VBA-Code ist die Beta-Funktion damit

Die Beta-Binomialverteilung kann nun für k
Ausfälle, n Kreditnehmer,
Ausfallwahrscheinlichkeit PD und
Ausfallkorrelation rho in VBA folgendermaßen
umgesetzt werden:

Wird in der obigen VBA-Funktion kum auf 1
gesetzt, so wird die kumulierte Verteilung berechnet.
Technischer Anhang
Beta-Binomialverteilung
Das Auftreten von \(k\) Ausfällen
ist mit der Beta-Binomialverteilung \[P(X=k)
= \binom{N}{k} \frac{B(\alpha+k, \beta + N -
k)}{B(\alpha,\beta)}.\] Dabei ist \[B(\alpha, \beta) = \int_0^1 x^{\alpha - 1}(1 -
x)^{\beta - 1} dx\] die Beta-Funktion.
Die Beta-Binomialverteilung hat den Erwartungswert \[E[X] = N \cdot
\frac{\alpha}{\alpha+\beta}\] und die Varianz \[Var[X] = N \cdot
\frac{\alpha\beta}{(\alpha+\beta)^2}\cdot
\frac{\alpha+\beta+N}{\alpha+\beta+1}\] Die
Beta-Binomialverteilung hat als Randverteilung die Binomialverteilung
\[
X|\pi \sim \binom{N}{x} \pi^x (1-\pi)^{N-x}\] und die
Beta-Verteilung \[\pi \sim
\text{Be}_{\alpha,\beta}.\] Mit \(\alpha=\text{PD} \cdot
\frac{1-\rho}{\rho}\) und \(\beta=(1-\text{PD}) \cdot
\frac{1-\rho}{\rho}\) ist \[E[X] = N
\cdot \frac{\alpha}{\alpha+\beta} = N \cdot \text{PD}\] und die
Korrelation \[\begin{aligned}
\rho(X_i,X_j) & = & \frac{1}{\alpha+\beta+1}\\
& = & \frac{1}{\text{PD} \cdot
\frac{1-\rho}{\rho}+(1-\text{PD}) \cdot \frac{1-\rho}{\rho}+1}\\
& = & \frac{1}{\frac{1-\rho}{\rho}+1}\\
& = & \frac{1}{\frac{1-\rho+\rho}{\rho}}\\
& = & \rho.
\end{aligned}\]
Defaultkorrelationen
Die Defaultkorrelationen können entweder auf verschiedene Werte
gesetzt werden (z.B. 1%, 2%, 3%) und so eine "’implizite
Defaultkorrelation"’ aus der Stichprobe ermittelt werden, d.h. die
Korrelation, die die beobachteten Ausfälle am Besten erklären, oder es
werden die aufsichtsrechtlichen Korrelationen benutzt.
Für \(R_A\) als
Assetkorrelation wie in (BIS CRE
2023) und für die bivariate Standardnormalverteilung \[\Phi_{\mu, \text{Cov}(x,y)}\] mit
Erwartungsvektor \(\mu=(0,0)^T\) und
Kovarianzmatrix \[Cov =
\left(\begin{array}{cc}
1 & R_A\\
R_A & 1
\end{array}\right)\] berechnet sich die Defaultkorrelation \(\rho\) zu \[\rho
= \frac{\Phi_{\mu, \text{Cov}(x,y)}\left(\Phi^{-1}(\text{PD}),
\Phi^{-1}(\text{PD})\right)-\text{PD}^2}{\text{PD} \cdot
(1-\text{PD})}.\] Dabei ist \(\Phi\) die Standardnormalverteilung.
Damit lassen sich Assetkorrelationen \(R_A\) aus Basel III in Defaultkorrelationen
\(\rho\) umrechnen.
Literatur
Andreas Henking, Christian Bluhm und Ludwig Fahrmeir. 2006. Kreditrisikomessung. Berlin: Springer.
BIS CRE. 2023. “CRE31 IRB Approach: Risk Weight Functions.” Bank for International Settlements. https://www.bis.org/basel_framework/chapter/CRE/31.htm?inforce=20230101&published=20200327&tldate=20230101.
Leonhard Held, Daniel Bove. 2020. Lilelihood and Bayesian Inference, 2nd Ed. Berlin: Springer.
Moraux, Franck. 2010. “Sensitivity Analysis of Credit Risk Measures in the Beta Binomial Framework.” The Journal of Fixed Income 2010 (Winter): 66–76.
Nick W Kraemer, Jon Palmer. 2023. “Default, Transition, and Recovery: 2022 Annual Global Corporate Default and Rating Transition Study.” https://www.spglobal.com/ratings/en/research/articles/230425-default-transition-and-recovery-2022-annual-global-corporate-default-and-rating-transition-study-12702145.