I. Stochastische Prozesse
In den nächsten drei Abschnitten werden die mathematischen Grundlagen für stochastische Prozesse, Wiener-Prozesse und stochastische Integrale dargestellt. Eine sehr gute Quelle und auch die Basis der folgenden Ausführungen ist das sehr gute Buch von (Björk 2020). Ausgangspunkt sind zunächst die stochastischen Prozesse:
Definition 1 (Stochastischer Prozess). Ein stochastischer Prozess \(X = \{X(t) : t \in T\}\) auf einem Wahrscheinlichkeitsraum \((\Omega, \mathcal{F}, P)\) ist eine Familie von Zufallsvariablen, wobei für jedes \(t\) in einer Indexmenge \(T\), \(X(t)\) eine Zufallsvariable ist, die von \(\Omega\) auf den reellen Zahlen (oder einem anderen Zustandsraum) definiert ist.
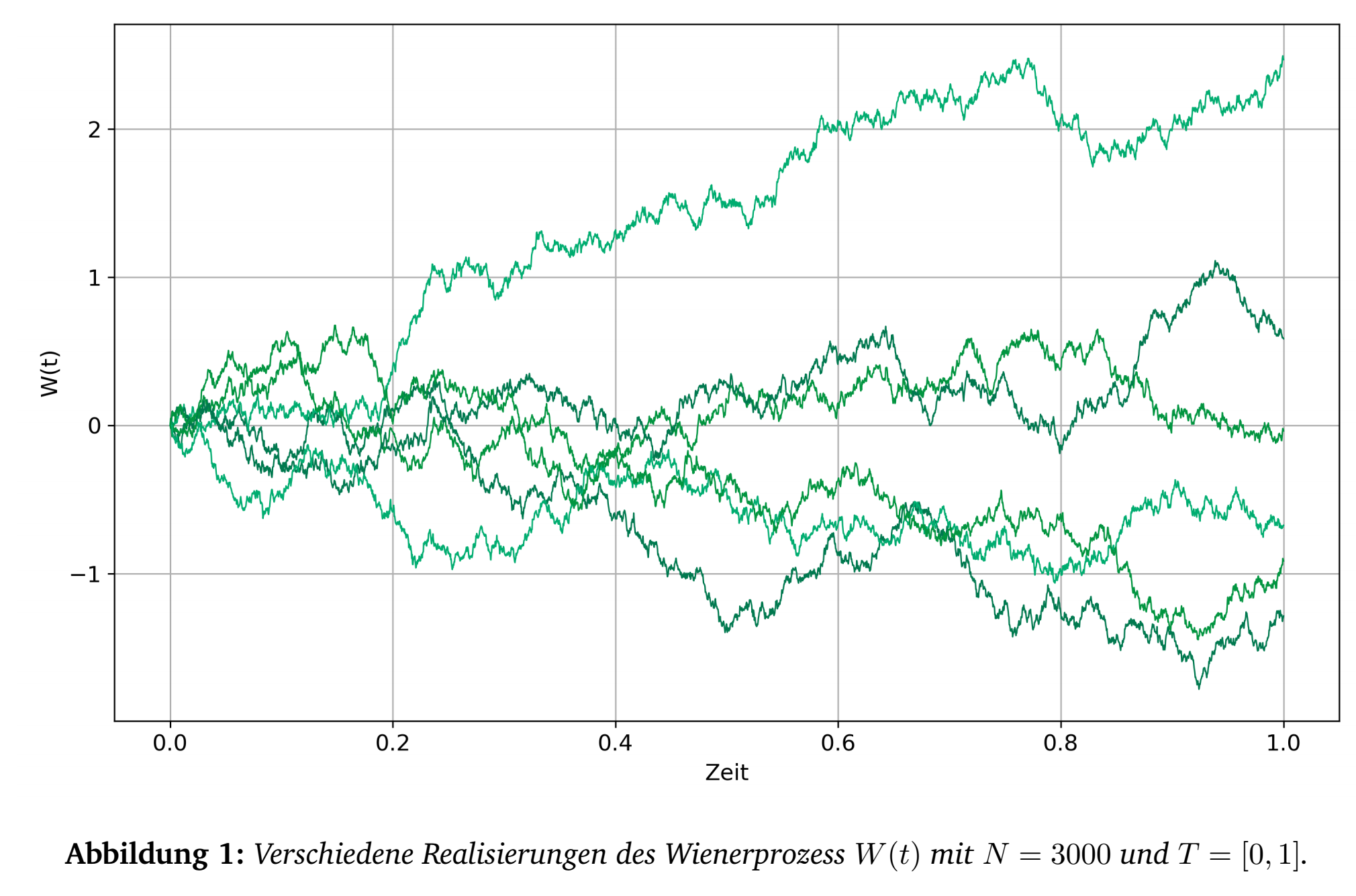
Oft ist es einfacher, sich die Indexmenge \(T\) als Zeit vorzustellen. Bei Stochastischen Prozessen wird also zu jedem Zeitpunkt \(t\) eine Zufallsgröße \(X(t)\) "’aktiv"’. Eine einzelne Realisation \(t \mapsto X(t)\) aus allen möglichen zufälligen Möglichkeiten wird auch Samplepfad genannt (vgl. Abbildung 1). Sind solche Realisierung immer stetig, spricht man von stetigen stochastischen Prozessen.
Das \({\cal F}\) in der Definition des stochastischen Prozesses ist eine \(\sigma\)-Algebra. Die \(\sigma\)-Algebra bestimmt, welche Ereignisse "’messbar"’ oder "’beobachtbar"’ sind. Ein Ereignis ist eine Teilmenge von \(\Omega\). Wenn ein Ereignis in der \(\sigma\)-Algebra enthalten ist, kann ihm eine Wahrscheinlichkeit zugeordnet werden. Ansonsten ist das Ereignis für die Wahrscheinlichkeitsverteilung von \(X(t)\) nicht existent.
Eine Filtration \(\mathbb{F}=(\mathcal{F}_t)_{t \geq 0}\) ist eine Familie von \(\sigma\)-Algebren, wobei \(\mathcal{F}_t\) die bis zur Zeit \(t\) verfügbare Information repräsentiert, d.h.für alle \(s \leq t\) gilt \(\mathcal{F}_s \subseteq \mathcal{F}_t\). Man sagt, ein stochastischer Prozess \(X = (X_t)_{t \geq 0}\) ist adaptiert an die Filtration, wenn für jedes \(t\), \(X(t)\) messbar bezüglich \(\mathcal{F}_t\) ist. Das bedeutet, dass der Wert von \(X(t)\) nur von den Informationen abhängt, die bis zur Zeit \(t\) verfügbar sind. Um die Sache einfacher zu machen, wählt man als Filtration \(\mathbb{F}=(\mathcal{F}_t)_{t \geq 0}\) meist die \(\sigma\)-Algebren \(\mathcal{F}_t\), für die jedes mögliche Ereignis von \(X(t)\) messbar ist. Diese heißt dann die von \(X(t)\) erzeugte Filtration. \(X(t)\) ist zu dieser Filtration per Definition adaptiert.
Wichtige Typen von stochastischen Prozessen sind Martingale. Bezeichnet man mit \({\cal F}_s\) die Menge aller möglichen Ereignisse bis zum Zeitpunkt \(s\) (mathematisch ist \({\cal F}_s\) eine \(\sigma\)-Algebra aus der Filtration \(\mathbb{F}\) zum Zeitpunkt \(s\)), dann gilt für einen Martingal-Prozess für \(t \geq s\): \[\mathbb{E}[X(t)|{\cal F}_s] = X(s),\] d.h. werden alle Informationen zum Zeitpunkt \(s\) einbezogen (diese sind in \({\cal F}_s\)), ist der Erwartungswert aller zukünftigen Realisierungen, so verteilt wie \(X(s)\), oder anders gesagt: neues Spiel, neues Glück.
II. Der Wiener-Prozess
Ein äußerst wichtiger stochastischer Prozess ist die Brownsche Bewegung bzw. gleichbedeutend der Wiener-Prozess:
Definition 2 (Wiener-Prozess). Ein stochastischer Prozess \(W(t)\) heißt Wiener-Prozess, wenn gilt:
\(W(0) = 0\).
Für alle \(0 \leq s < t\) ist \(W(t) - W(s)\) unabhängig von der Vergangenheit, das heißt unabhängig von allen Werten \(W(u)\) mit \(u \leq s\).
Für alle \(0 \leq s < t\) ist \(W(t) - W(s)\) normalverteilt mit Erwartungswert 0 und Varianz \(t-s\), also \[W(t) - W(s) \sim \mathcal{\phi}(0, t-s).\]
Mit Wahrscheinlichkeit 1 ist der Pfad von \(W(t)\) stetig in \(t\) für alle \(t \geq 0\).
Bemerkung 3. Mit \(s=0\) zeigt Punkt 3 obiger Definition, dass \(W(t)\) selbst mit Erwartungswert \(0\) und Varianz \(t\) normalverteilt ist.
Zudem gilt mit \(s < t\) folgendes: \[\begin{aligned} \mathbb{E}(W(t)^2 \mid \mathcal{F}_s) &= \mathbb{E}\left( [W(s) + (W(t) - W(s)]^2 \mid \mathcal{F}_s \right) \\ &= W(s)^2 + 2W(s) \mathbb{E}[W(t) - W(s) \mid \mathcal{F}_s] \\ &\quad + \mathbb{E}[(W(t) - W(s))^2 \mid \mathcal{F}_s] \\ &= W(s)^2 + 0 + (t-s) . \end{aligned}\] \(W(t)^2 - t\) ist somit ein Martingal.
Folgender Beispiel-Code zeigt, wie ein Wiener-Prozess mit \(W(0)=0\) simuliert werden kann:

Abbildung 1 zeigt einige Realisierungen eines Wiener-Prozesses:
III. Die Ito-Formel
Stochastische Prozesse \(X(t)\) können meist auch als Veränderungsprozess (stochastisches Differential)f1 beschrieben werden, d.h. ist ein kleiner Zeitabschnitt \(\Delta t\) gegeben, wie verändert sich dann der Prozess \(X(t+\Delta t)\).
Für \(\Delta t \rightarrow 0\) schreibt man dann bei Prozessen an denen als stochastische Komponente ein Wienerprozess \(W(t)\) beteiligt ist: \[dX(t) = g(t) dt + Y(t)dW(t).\] Dabei sind \(g(t), Y(t)\) ebenfalls stochastische Prozesse. Zur Lösung muss integriert werden. Während das erste Integral nach gewöhnlichen Methoden integriert werden kann, muss man für das zweite eine sinnvolle Integrationsdefinition finden. Für einfache Prozesse, d.h. \(Y(s)\) ist stückweise deterministisch zwischen \(t_k\) und \(t_{k+1}\), \(k=0, \dots n\), \(t_0 = a\), \(t_n=b\), wäre \[\sum_{k=0}^{n-1} Y(t_k)\left[W(t_{k+1})-W(t_k)\right] .\] ein sinnvoller Intergralbegriff. Ist \(Y(s)\) nicht stückweise deterministisch, so kann man ihn durch stückweise deterministische Prozesse \(\{\tilde{Y}_n\}\) approximieren. Das Ito-Integral ist dann definiert als \[\int_a^b Y(s) d W_s=\lim _{n \rightarrow \infty} \int_a^b \tilde{Y}_n(s) d W(s)\] Mit \[X(t)=\int_0^t Y(s) dW(s)\] ist das Ito-Integral wieder ein stochastischer Prozess. Zudem kann gezeigt werden, dass es die Martingal-Eigenschaft hat, d.h. mit \(t > s\) \[E(X(t)| {\cal F}_s^W) = X(t).\] Im Folgenden soll nun mit \(\mu(s), \sigma(s)\)f2 folgender stochastische Prozess \[X(t) = a + \int_0^t \mu(s) ds + \int_0^t\sigma(t)dW(s)\] betrachtet werden. Dies ist offensichtlich die Lösung des stochastischen Differntials \[dX = \mu(t)dt + \sigma(t) dW_t\] mit dem Startpunkt \(X(0) = a\). Obiger Prozess wird auch Ito-Prozess genannt.
Für Ito-Prozesse gilt folgendes Theorem, das auch Ito-Formel genannt wird (vgl. (Björk 2020), Theorem 4.11, p. 54):
Theorem 4 (Ito-Formel). Sei \(X(t)\) ein Ito-Prozess mit \(X(t) \in \mathbb{R}\), \(t \in [0,T]\). Für eine Funktion \(f: T \times \mathbb{R} \longrightarrow \mathbb{R}\), \(f \in C^{1,2}\), d.h. \(f(t,x)\) in \(t\) einmal und in \(x\) zweimal differenzierbar, gilt dann: \[df\left(t, X(t)\right)=\left\{\frac{\partial f}{\partial t}\left(t, X(t)\right)+\mu(t) \frac{\partial f}{\partial x}\left(t, X(t)\right)+\frac{1}{2} \sigma(t)^2 \frac{\partial^2 f}{\partial x^2}\left(t, (t)\right)\right\} d t+\sigma(t) \frac{\partial f}{\partial x}\left(t, X(t)\right) dW(t) .\]
Die Ito-Formel ist ein mächtiges Werkzeug und soll nachfolgend auf die in der Finanzmathematik sehr bedeutsamen Geometrischen Brownschen Bewegung angewandt werden.
IV. Geometrische Brownsche Bewegung
Das stochastische Differential mit \(\mu, \sigma \in \mathbb{R}, \sigma \geq 0\) \[dX(t) = \mu X(t) dt + \sigma X(t) dW(t) = (\mu + \sigma dW(t))X(t)\] und \(X(0)=x_0\) heißt Geometrische Brownsche Bewegung.
Für \(\sigma=0\) verschwindet der stochastische Teil und die Lösung wäre in diesem Fall: \[X(t) = x_0 e^{\mu t}.\] Es soll die Ito-Formel mit \(f(t,X(t)) = \ln(X(t))\) benutzt werden. \(f\) ist in \(C^{1,2}\) und erfüllt damit die Voraussetzung der Ito-Formel. Da \(f\) nur von \(X(t)\) abhängig und nicht zusätzlich von einer weiteren Zeitkomponente \(t\) ist hier \(\frac{\partial f}{\partial t}(t,X(t)) = 0\). Mit \(\mu(t)=\mu X(t)\) und \(\sigma(t)=\sigma X(t)\) ist die geometrische Brownsche Bewegung auch ein Ito-Prozess, d.h. alle Voraussetzungen für die Ito-Formel sind erfüllt. Also ist \[\begin{aligned} df\left(t, X(t)\right) & = & \left\{\frac{\partial \ln}{\partial t}\left(t, X(t)\right)+\mu(t) \frac{\partial \ln}{\partial x}\left(t, X(t)\right)+\frac{1}{2} \sigma(t)^2 \frac{\partial^2 \ln}{\partial x^2}\left(t, X(t)\right)\right\} d t\\ & & +\sigma(t) \frac{\partial \ln}{\partial x}\left(t, X(t)\right) dW(t)\\ & = & \left\{0+\mu(t) \frac{1}{X(t)} -\frac{1}{2} \sigma(t)^2 \frac{1}{X(t)^2} \right\} dt+\sigma(t) \frac{1}{X(t)}dW(t)\\ & = & \left\{\mu X(t) \frac{1}{X(t)} -\frac{1}{2} \sigma^2 X(t)^2\frac{1}{X(t)^2} \right\} dt+\sigma X(t) \frac{1}{X(t)}dW(t)\\ & = & \left(\mu - \frac{\sigma^2}{2}\right) dt +\sigma dW(t) \end{aligned}\] Dies kann direkt integriert werden, also \[f\left(t, X(t)\right)=\ln(X(t)) = \ln(x_0) + \left(\mu - \frac{\sigma^2}{2}\right) t + \sigma W(t)\] und damit \[X(t) = x_0 \exp\left(\left(\mu - \frac{\sigma^2}{2}\right) t + \sigma W(t)\right).\] Nachdem dieses Ergebnis in der Finanzmathematik sehr wichtig ist, wird es im folgendem Lemma festgehalten:
Lemma 5. Für den stochastischen Prozess \[dX(t) = \mu X(t) dt + \sigma X(t) dW(t) = (\mu + \sigma dW(t))X(t)\] mit \(X(0)=x_0\) ist \begin{equation}X(t) = x_0 e^{\left(\mu - \frac{\sigma^2}{2}\right) t + \sigma W(t)}.\end{equation} eine Lösung. Zudem ist der Erwartungswert \[\mathbb{E}[X(t)] = x_0 e^{\mu t}.\]
Beweis: Der erste Teil wurde bereits gezeigt. Für den Erwartungswert gilt: \[\begin{aligned} \mathbb{E}[X(t)] &= \mathbb{E}\left[x_0 e^{\left(\mu - \frac{\sigma^2}{2}\right) t + \sigma W(t)}\right]\\ & = x_0 \mathbb{E}\left[e^{\left(\mu - \frac{\sigma^2}{2}\right) t} \cdot e^{\sigma W(t)}\right]\\ & = x_0 e^{\left(\mu - \frac{\sigma^2}{2} t\right)} \cdot \mathbb{E}\left[e^{\sigma W(t)}\right] \end{aligned}\] Nach Bemerkung 3 ist \(W(t)\) normalverteilt mit Erwartungswert \(0\) und Varianz \(t\). Damit ist \(\sigma W(t)\) normalverteilt mit Erwartungswert \(0\) und Varianz \(\sigma^2 t\). Nach Satz 6 ist damit \[\mathbb{E}\left[e^{\sigma W(t)}\right] = e^{0+\frac{\sigma^2 t}{2}}.\] □

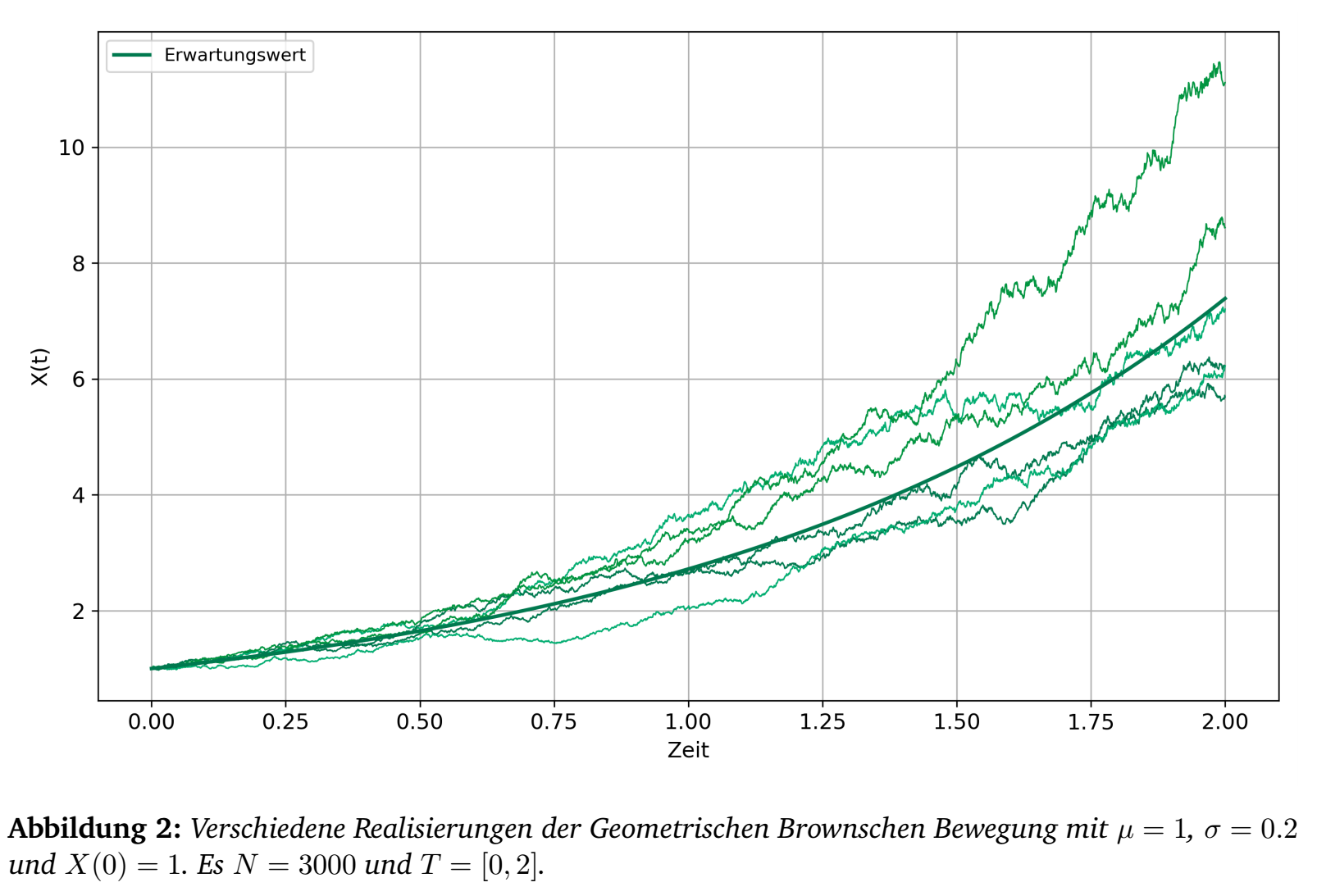
Abbildung 2 zeigt einige Realisierungen einer Geometrischen Brownschen Bewegung.
V. Zusammengesetzte Wiener-Prozesse
Es ist möglich, aus der Addition zweier Wiener-Prozesse \(W_1(t), W_2(t)\) wieder einen Wiener-Prozess \(W(t) = a W_1(t)+b W_(t)\) zu kreieren. Allerdings ist die Wahl von \(a,b\) hier nicht frei aus den reelen Zahlen zu wählen. 1., 2. und 4. sind aus Definition 2 offensichtlich für \(W(t)\) erfüllt. Zudem ist \(W(t)\) als linear Kombination aus den normalverteilten Zufallsgrößen \(W_1(t)\) und \(W_2(t)\) wieder normalverteilt und der Erwartungswert ist \(0\) (vgl. Satz 7 im Anhang). Es bleibt also zu zeigen, dass die Varianz von \(W(t)=t\) ist.
Es ist \[\begin{aligned} Var[W(t)] & = Var[a W_1(t)+b W_2(t)] \\ &= a^2 Var[W_1(t)] +b^2 Var[W_2(t)]\\ &= a^2 t + b^2 t\\ &= (a^2+b^2) t \end{aligned}\] Für \(a^2 + b^2 = 1\) ist somit \(W(t)\) ein Wiener-Prozess oder anders ausgedrückt wegen \(\text{Var}[c X] = c^2 \text{Var}[X]\) ist auch:
\begin{equation}W(t) = \frac{1}{\sqrt{a^2 + b^2}} \left(a W_1(t)+b W_2(t)\right)\end{equation} ein Wiener-Prozess.
Im Anhang wird gezeigt, dass obige Überlegungen auf einen \(n\)-dimensionalen Wiener-Prozess, der sich aus der Summe von \(d\) Wiener-Prozessen zusammensetzt, verallgemeinert werden kann.
VI. Modellierung des Unternehmenswertes
Im folgenden wird nun angenommen, dass der Wert \(V_t\) eines Unternehmensf3 einen erwarteten Zuwachs von \(\mu\) hat. Das Risiko der Wertentwicklung soll in zwei unabhängige Risiken aufgeteilt werden, nämlich der wirtschaftlichen Gesamtentwicklung (systematisches Risiko) \(\alpha\) und der idiosynkratischen Entwicklung (unsystematisches bzw. spezifisches Risiko) \(\beta\).
Mathematisch folgt der Unternehmenswert dann folgendem Prozess: \begin{equation} dV_t = \mu V_t dt + \alpha V_t d W_1(t) + \beta V_t d W_2(t).\end{equation} Der Prozess ist nach (2) gleichbedeutend zu \[dV_t = \mu V_t dt + \sqrt{\alpha^2+\beta^2} V_t d W(t),\] wobei \(W(t)\) Wiener-Prozess mit \begin{equation} W(t) = \frac{1}{\sqrt{\alpha^2 + \beta^2}} \left(\alpha W_1(t)+\beta W_2(t)\right)\end{equation} ist. Es kann nun Lemma 5 angewandt werden und man erhält folgenden stochastischen Prozess: \[V_t = V_0 e^{\left(\left(\mu - \frac{\alpha^2+\beta^2}{2}\right) t + \sqrt{\alpha^2+\beta^2} W(t)\right)}.\] Der Unternehmenswert \(V_t\) bildet die gesamte Aktivseite ab. Falls der Unternehmenswert unter die Verpflichtungen auf der Passiv-Seite \(L\) fällt (d.h. das Eigenkapital als Residualgröße ist kleiner \(0\)), liegt ein Ausfall vor.
Mathematisch formuliert ist damit Ausfallwahrscheinlichkeit \(p_t\) gleichbedeutend mit der Wahrscheinlichkeit, dass \(V_t\) unter \(L\) liegt: \[\begin{aligned} p_t & = P\left(V_0 e^{\left(\mu - \frac{\alpha^2+\beta^2}{2}\right) t + \sqrt{\alpha^2+\beta^2} W(t)}<L\right)\\ & = P\left(\left(\mu - \frac{\alpha^2+\beta^2}{2}\right) t + \sqrt{\alpha^2+\beta^2} W(t)<\ln\left(\frac{L}{V_0}\right)\right).\\ & = P\left( W(t)<\frac{\ln\left(\frac{L}{V_0}\right)-\left(\mu - \frac{\alpha^2+\beta^2}{2}\right) t}{\sqrt{\alpha^2+\beta^2}} \right)\\ \end{aligned}\] Es soll nun der Fall \(t=1\) betrachtet werden. Dann ist \(p_t\) die Ausfallwahrscheinlichkeit für 1 Jahr und \(W(1)\) ist gemäß Definition eine standardnormalverteilte Zufallsgröße mit Verteilungsfunktion \(\Phi(x)\) , d.h. obige Formel - und damit die Ausfallwahrscheinlichkeit für 1 Jahr \(p_1\) - vereinfacht sich zu \begin{equation} p_1 = \Phi\left( \frac{\ln\left(\frac{L}{V_0}\right)-\mu + \frac{\alpha^2+\beta^2}{2}}{\sqrt{\alpha^2+\beta^2}} \right).\end{equation}
VII. Die RWA-Formel nach Basel
Formel (5) ist beispielsweise Grundlage für Modelle wie KMV. Hier werden Ausfallwahrscheinlichkeiten auf Basis von Volatilitäten und anderen Inputparameter abgeleitet und eine "Distance To Default" berechnet. Bei Banken werden die Ausfallraten allerdings meist über Ratingstools ermittelt, d.h. bei Banken ist \(p:=p_1\) abgeleitet aus einem Ratingverfahren für einen Kreditnehmer vorhanden. Es kann daher \[\Phi^{-1}(p) = \frac{\ln\left(\frac{L}{V_0}\right)-\mu + \frac{\alpha^2+\beta^2}{2}}{\sqrt{\alpha^2+\beta^2}}\] ermittelt werden und damit muss \(W(1)\) nach (5) gleich oder kleiner \(\Phi^{-1}(p)\) sein, damit ein Ausfall stattfindet.
Definiert man nun \(\rho = \frac{\alpha^2}{\alpha^2+\beta^2}\), dann ist \(1-\rho = \frac{\beta^2}{\alpha^2+\beta^2}\) und mit (2) gilt \[W(t)=\sqrt{\rho}\cdot W_1(t) + \sqrt{1-\rho}\cdot W_2(t).\] Für \(t=1\) sind sowohl \(W_1(t)\) als auch \(W_2(t)\) standardnormalverteilt.
Zur Vereinfachung der folgenden Nomenklatur, soll die Bernoulli-Zufallsgröße \(D\) mit \(D =1\), falls ein Ausfall vorliegt und \(D=0\), falls kein Ausfall vorliegt, definiert werden.
Offensichtlich ist \(P(D=1) = p\) oder gleichbedeutend \[P(D=1)=P\left(W(1)=\sqrt{\rho} \cdot W_1(1) + \sqrt{1-\rho} \cdot W_2(1) <\phi^{-1}(p)\right).\] Es soll nun für den systematischen Teil \(\alpha V_t d W_1(t)\) des ursprünglichen Prozesses (3) ein Ereignis vorgegeben werden, z.B. \(W_1(1) = y\), und die bedingte Wahrscheinlichkeit \(P(D=1|W_1(1)=y)\) berechnet werden. Es ist \[\begin{aligned} P(D=1|W_1(1)=y) & = P\left(\sqrt{\rho} y + \sqrt{1-\rho} W_2(1) \leq \Phi^{-1}(p)\right)\\ & = P\left(W_2(1) \leq \frac{\Phi^{-1}(p)- \sqrt{\rho} y}{\sqrt{1-\rho}}\right). \end{aligned}\] Da \(W_2(1)\) standardnormalverteilt ist, ist dies gleichbedeutend mit \begin{equation} P(D=1|W_1(1)=y) = \Phi\left(\frac{\Phi^{-1}(p)- \sqrt{\rho} y}{\sqrt{1-\rho}} \right).\end{equation} Gibt es kein systematisches Risiko, d.h. \(\rho=0\), so ist \[P(D=1|W_1(1)=y) = \Phi\left(\frac{\Phi^{-1}(p)- \sqrt{0} y}{\sqrt{1-0}}\right)=\Phi\left(\Phi^{-1}(p)\right) = p.\] Formel (6) wird Baselformel genannt. Bei der Baselformel wird der systematische Teil gestresst, d.h. es wird die veränderte Ausfallwahrscheinlichkeit berechnet, falls es ein Event für einen systematischen Abschwung gibt, der gemäß Modell in nur 1 von 1000 Fällen zu erwarten ist, d.h. \(y = \Phi^{-1}(0.001) = -\Phi^{-1}(0.999) \approx -3.09023\) (vgl. (10) im Anhang).
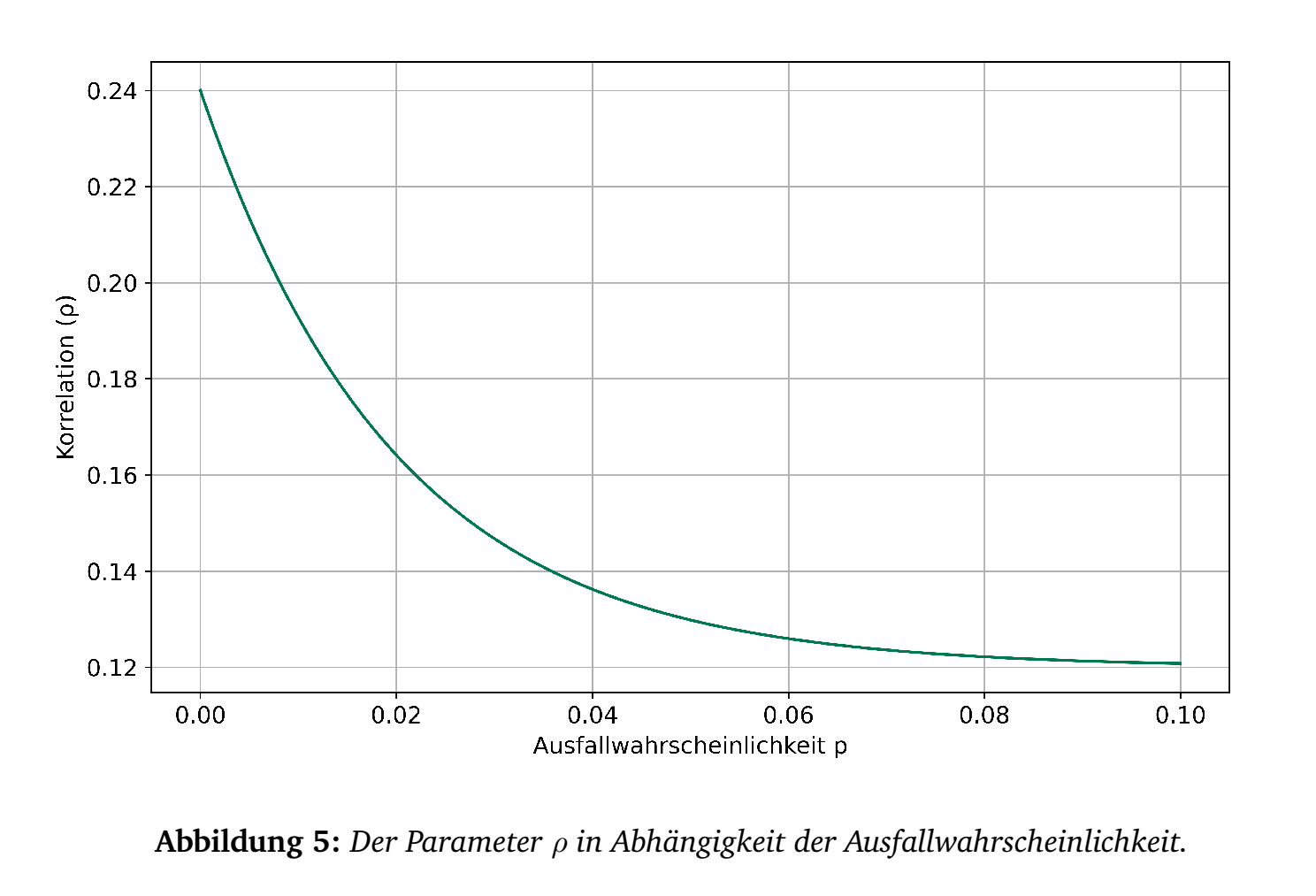
Den systematischen Teil anstelle dem spezifischen Teil einen Stress zu unterziehen ist durchaus sinnvoll. Nachdem ein Kreditinstitut eine Vielzahl von Krediten und unterschiedliche Schuldner hat, sind unerwartete Ausfälle aus dem spezifischen Teil (Gesetz der großen Zahlen) durch Diversifikation weitestgehend eliminiert. Was bleibt ist das systematische Risiko. In wie weit ein Unternehmen dem systematischen Risiko ausgesetzt ist, wird über den Faktor \(\rho\) definiert. Je höher \(\rho\), desto mehr hängt der Unternehmenswert vom systematischen Umfeld ab. \(\rho\) ist schwer zu schätzen und wird daher aufsichtsrechtlich für verschiedene Schuldnertypen vorgegeben.
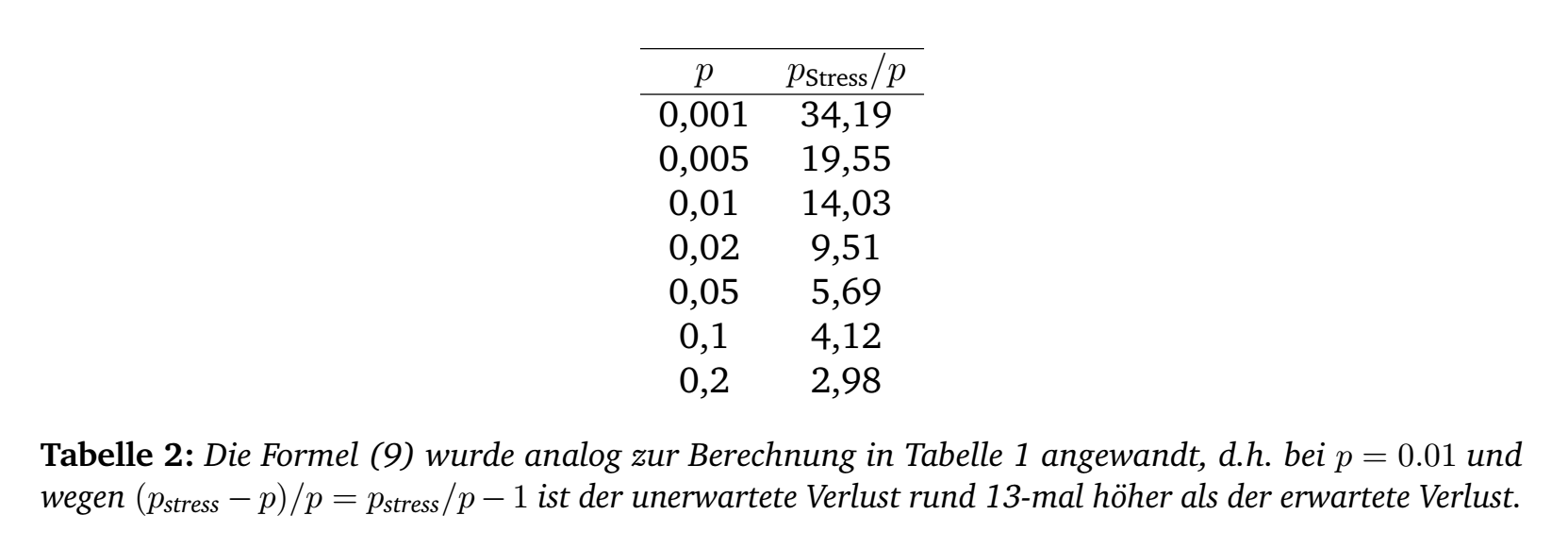
Folgende Tabelle gibt für unterschiedliche Ausfallwahrscheinlichkeiten und unterschiedlichen Abhängigkeiten zum systemischen Risiko \(\rho\), das Verhältnis des unerwarteten Ausfallrisiko gemäß Formel (6) gegenüber der erwarteten Ausfallwahrscheinlichkeit \(p\) an:
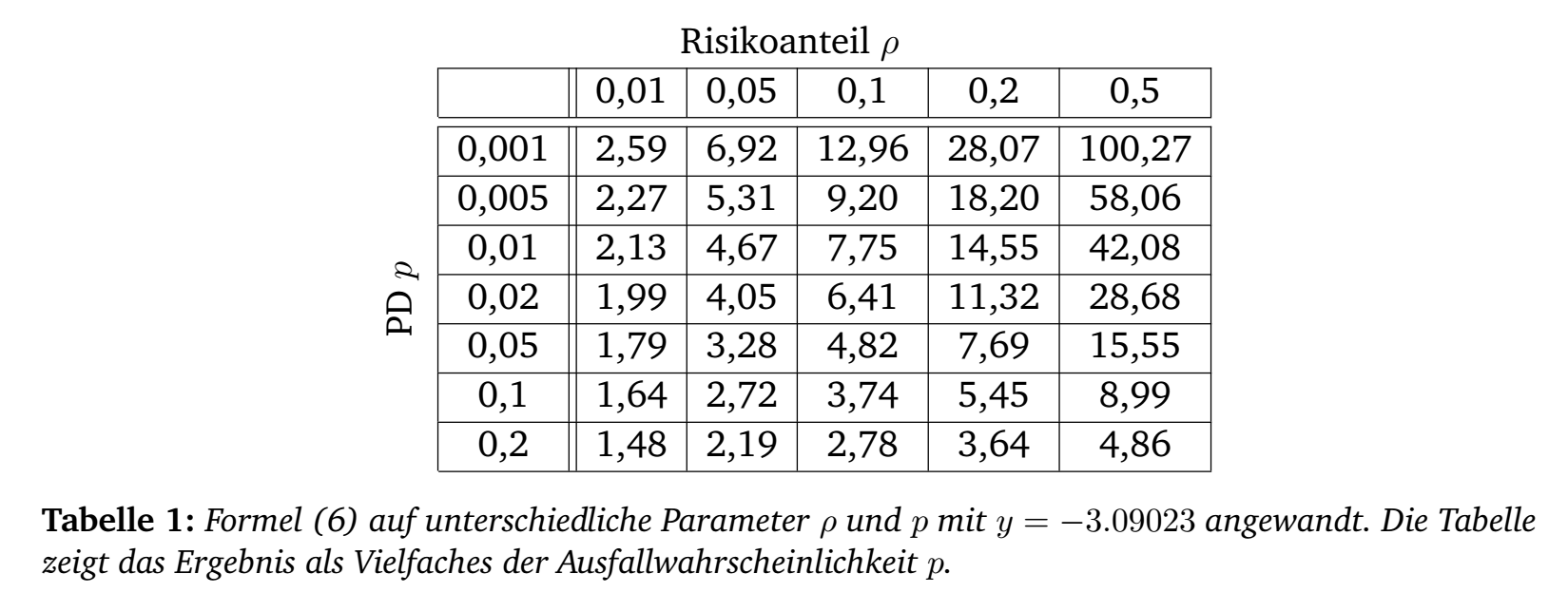
Je höher die Abhängigkeit \(\rho\) zum systematischen Risikos, desto größer der unerwartete Ausfall. Bei steigender erwartetenen Ausfallrate \(p\), wird das Verhältnis entsprechend kleiner. Beides ist wirtschaftlich durchaus nachvollziehbar.
Die Basel-Formel (6) berechnet eine Ausfallwahrscheinlichkeit unter Stress. Der erwartete Verlust aus einem Exposure mit Ausfallwahrscheinlichkeit \(p\) ist offensichtlich \[\text{EAD}\cdot \text{LGD} \cdot p.\] Dabei ist EAD das Exposure at Default und LGD als Loss Given Default der Anteil, der im Falle eines Ausfalls verloren geht. Auch zur Ermittlung von LGD und EAD werden von der Aufsicht Vorgaben gemacht, wobei im Advanced-Ansatz das Kreditinstitut eigene Schätzungen vornehmen kann.
Die Formelf4 \begin{equation} \text{EAD}\cdot \text{LGD}\cdot \left(\Phi\left(\frac{\Phi^{-1}(p)+ \sqrt{\rho}\cdot \Phi^{-1}(0.999)}{\sqrt{1-\rho}} \right)-p\right)\end{equation} gibt den unerwarteten Verlust für 1 Jahr an. Dabei ist das Konfidenzniveau für den systematischen Faktor \(99.9\%\).
Der erwartete Verlust muss bilanziell (IFRS 9) als Wertberichtigung für die erwarteten Kreditverluste berücksichtigt werden. Der unerwartete Verlust wird dagegen nicht bilanziert, sondern muss aufsichtsrechtlich mit Kapital unterlegt werden. Allerdings verlangt die Aufsicht (anders als IFRS9, in dem nur der erwartete Ausfall der nächsten 12 Monate berücksichtigt wird), dass länger laufende Kredite ein höheres unerwartetes Risiko aufweisen und damit mit zusätzlichem Kapital unterlegt werden müssen. Daher wird ein Laufzeitfaktor eingeführt.
Auch hier gibt es folgende Vorgaben:
Sei \(b=(0.11852-0.05478 \cdot \ln(p))^2\) und \(M\) die effektive Fälligkeit eines Kredites, d.h. \[M=\frac{\sum t \cdot CF_t}{\sum CF_t}\] mit \(t\) Zeitpunkt und \(CF_t\) Höhe eines Cash Flows aus dem Kredit. Aufsichtsrechtlich muss \(M\) immer zwischen \(1\) und \(5\) Jahre liegen, hat also einen Floor und einen Cap. Im Foundation-Ansatz werden 2.5 Jahre verwendet.
Mit dem Maturity Adjustment \[\text{MA} = \frac{1+(M-2.5)b}{1-1.5 b} = \frac{b}{1-1.5 b} M + \frac{1-2.5 b}{1-1.5 b}\] wird (7) abschließend multipliziert. Für gegebenes \(p\) ist \(b\) fixiert. Dann ist MA eine lineare Funktion von \(M\).
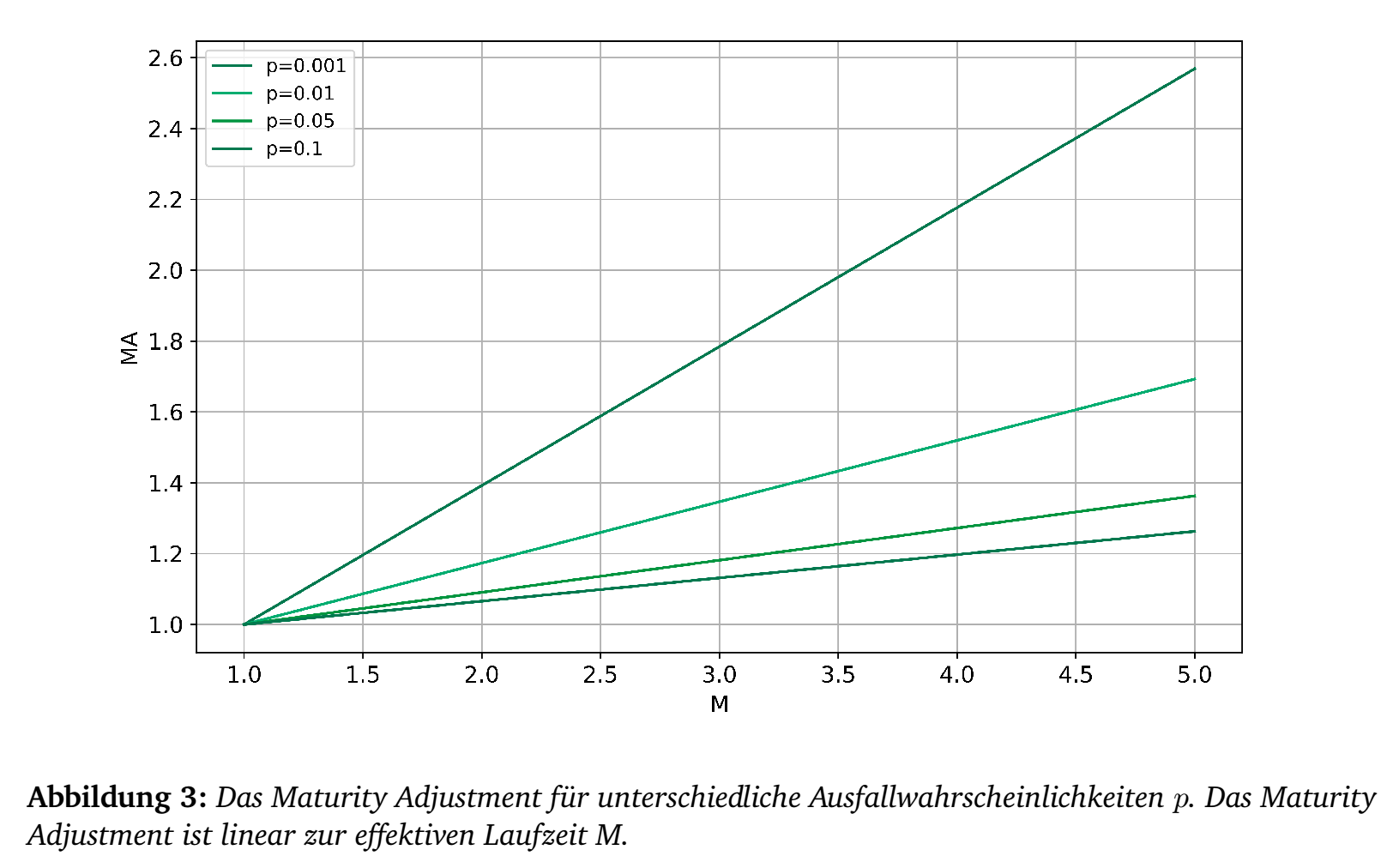
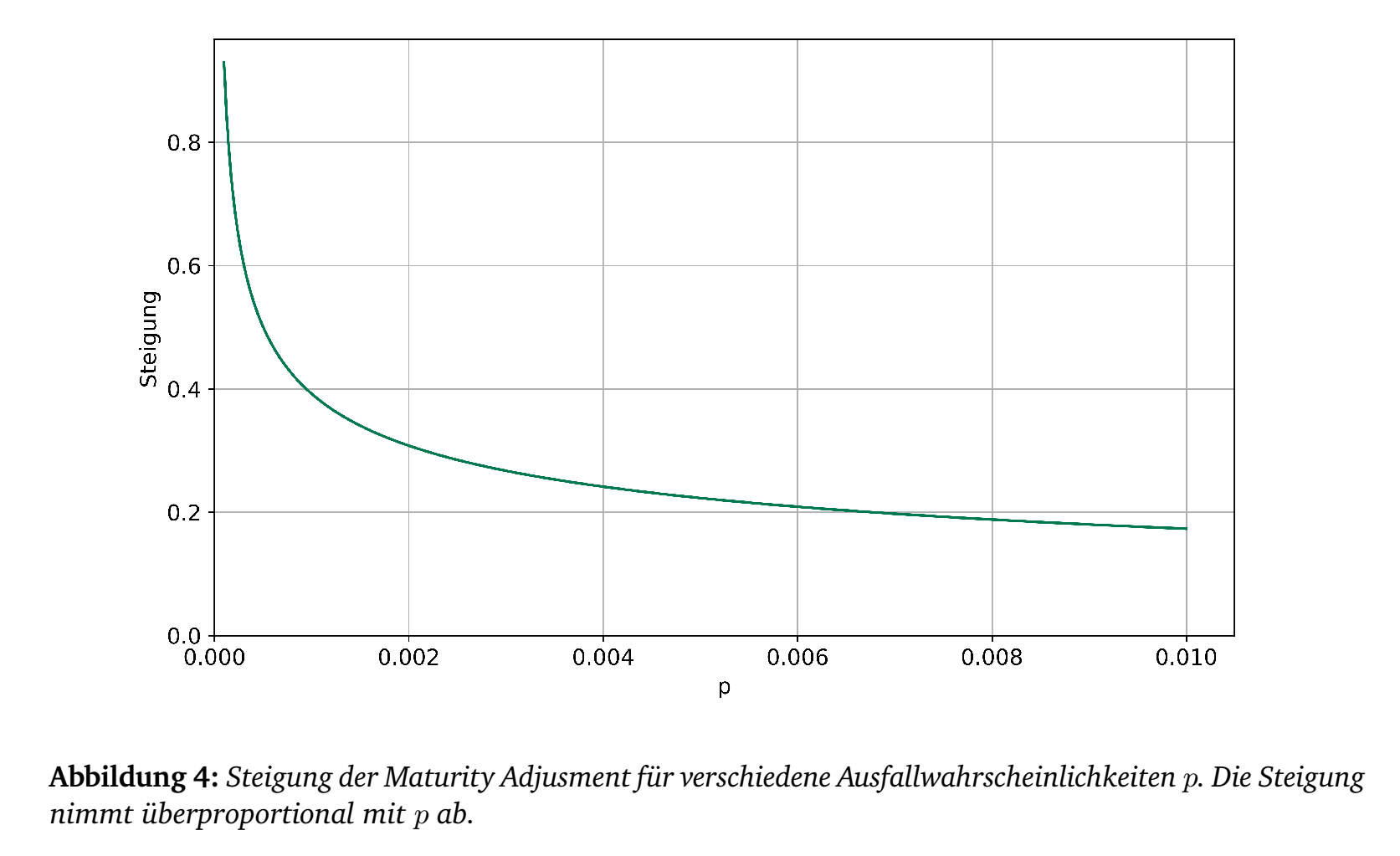
Aus mehr oder weniger historischen Gründen wird der Kapitalbedarf aus den Risk Weighted Assets bzw. RWA gebildet. Es soll Kapital in Höhe von \(8\%\) der RWA hinterlegt werden. Dementsprechend wird die Formel (7) neben der Multiplikation mit dem Maturity Adjustment MA noch mit dem Faktor 12.5 (=8% aus 100) ergänzt, um eine Formel für die RWA zu erhalten: \begin{equation} \text{RWA} = 12.5 \cdot \text{MA} \cdot\text{EAD}\cdot \text{LGD}\cdot \left(\Phi\left(\frac{\Phi^{-1}(p)+ \sqrt{\rho}\cdot \Phi^{-1}(0.999)}{\sqrt{1-\rho}} \right)-p\right).\end{equation} Der Parameter \(\rho\) wird von der Aufsicht vorgegeben und ist abhängig von \(p\). Die Formel hierzu ist \begin{equation} \rho = 0.12 \cdot \frac{1-e^{-50 \cdot p}}{1-e^{-50}} + 0.24 \cdot \left(1 - \frac{1-e^{-50 \cdot p}}{1-e^{-50}}\right)\end{equation} Aufsichtsrechtlich wird \(\rho\) für manche Branchen (u.a. Großbanken, Commercial Real Estate, Privatkunden) angepasst. Für einige Kredittypen (z.B. Immobilienkredite, Privatkunden) entfällt das Maturity Adjustment, d.h. MA=1.